The Alleynian Review: Mathematical Mindsets for Future Success

Mathematical Mindsets for Future Success
Your experiences of learning mathematics through your schooling have a lasting impact. I vividly remember my teachers in primary school and the positive effect they had on my relationship with mathematics. They encouraged me to explore mathematics as a creative subject and to gain a firm grasp of the core skills. Instilling a mathematical mindset early in a student’s education is essential. Mindset can affect one’s self-belief and self-efficacy. Of course, it is the desire of educators to provide the foundations for every student to prosper. As we know, it is true that not every child enjoys mathematics and that they can find it a challenging subject. So, how can we develop a mathematical mindset in every student?
Focus on Growth
Mindset can be considered a barrier to learning. Research by Dweck (2012) is widely referenced in education; it indicates that the mindset of a learner has been shown to have a measurable impact on learning, including enhancing both IQ and attainment. Learners have a mindset which is fixed or growth-oriented. However, mindset can be modified to have a positive impact on learning. Researchers highlight that a fixed mindset can make learners risk-averse and less likely to persevere with challenging tasks, limiting their learning potential.
How do you instil a mathematical mindset?
A mathematical mindset supports all learners to achieve the highest levels of attainment. This is a core value that influences our every day. We put the students first in our lesson designs and feedback. We support them with the belief that every student has the potential to achieve the highest levels. Moreover, we know that a fixed mindset can limit both a student’s engagement with mathematics and the depth of their mathematical conceptual understanding. Brain growth occurs with training and interventions, due to brain plasticity. A growth mindset can help to overcome a barrier in mathematics as it supports brain growth and resilience, developing persistence and a positive approach. The realisation that there is no such thing as a ‘maths brain’ can be a game-changing moment for students.
Boaler (2012) describes the following positive norms to encourage a growth mindset in students:
1. A belief that everyone can learn maths to the highest level
2. Mistakes are valuable (they grow your brain!)
3. Students should question to further their understanding
4. Maths is about creativity and making sense
5. Maths is about connections and communicating
6. Value depth of understanding over speed
7. Maths is about learning, not performing
To elaborate on a key point, valuing depth of understanding over speed allows students to reason in detail, making stronger connections and longer-term pathways in the brain.
Is mathematics not about practice and repetition to consolidate understanding? Research shows that the quality of the practice is most important. For example, a student completing an example of a formal written method, with a detailed verbal and written explanation, and visual representations, is more likely to retain that knowledge and apply the learning in a novel context than a child who has practised a method following a purely procedural repetitive approach. Quality of conceptually-based practice should be prioritised.
Junior School Mathematics: Progression in Problem-solving
To support the students’ development of mathematical mindsets, the Junior School at Dulwich College (Singapore) has implemented a structured problem-solving programme utilising heuristics, which are general methods to solve problems or rules of thumb (see Figure 1). The students use the strategies as starting points, as ways to navigate through a challenging problem and to alter their approach. Heuristics are powerful tools which develop mental models to support the student in tackling more abstract, open-ended and real-world problems. They enhance resilience and perseverance. The students develop intuition in their mathematics and learn how to navigate their way through an apparent dead-end. These skills are essential in Junior School mathematics, but also far beyond.
The progression targets the development of mathematical mindsets, promoting the transfer and application of learning. In addition, the curriculum design also supports interleaving of the curriculum and retention of learning. Furthermore, this gives the student the opportunity to explore mathematics and collaborate to achieve a positive outcome. The poster below was developed through the mathematics vertical strategic group in the Junior School. It is used throughout the Junior School to allow students to progressively develop and apply the strategies.

Figure 1: A poster to aid the development and application of mathematical strategies
How do you teach problem-solving?
Prior knowledge is an integral aspect of problem-solving. The Junior School mathematics programme provides structured support for students to gain the core foundations required for effective problem-solving. In problem-solving lessons, teachers model and show worked examples of potential methods. The aim is for students to gain the understanding and experience of using heuristics. A Year 3 student may need more support and modelling, whilst a Year 6 student will aim to become more autonomous in using and applying the strategies. There is a progression from scaffolding to more independence.
Schematic mental models for problem-solving, cognitive structures that link concepts and represent relationships among those concepts, enable future application to unknown scenarios. They are more sophisticated in experts and are developed through deliberate practice. Sweller (1988) proposed that schematic development is imperative because it ensures that the working memory’s capacity is not exceeded. Without a mathematical mindset, the working memory can be impaired due to anxiety, which can be inhibitory in the problem-solving process.
Low Threshold, High Ceiling Tasks
A focus on growth promotes a positive mindset, enhancing resilience and perseverance in learners of all levels of achievement. The notion of a mathematical mindset motivates and encourages students to work cooperatively and collaboratively, which supports a more equitable learning environment for mathematics. In the Junior School, students are encouraged to explore and discover solutions. One of the most amazing parts of being a teacher is witnessing those ‘AHA!’ moments when a solution to a challenging problem is found. In class-based mathematics, low threshold, high ceiling problem-solving activities promote mathematical mindsets.
The problem below (Figure 2) is an example of a low threshold, high ceiling task.
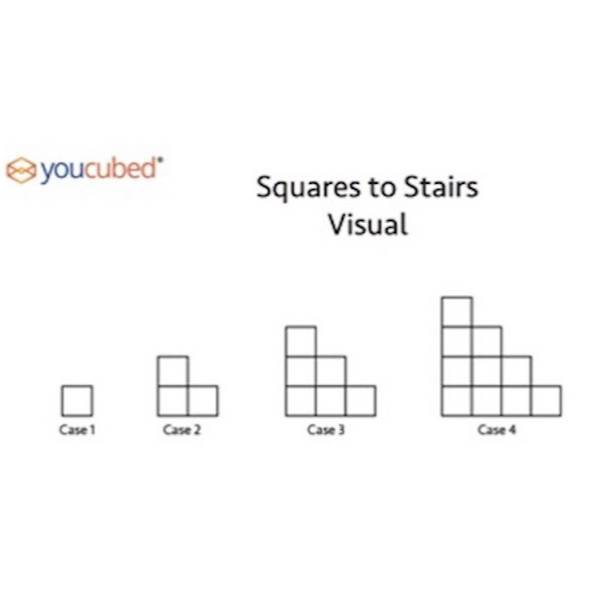
Figure 2: The squares to stairs task (Youcubed, 2020)
Possible questions relating to Squares to Stairs Visual problem:
- What would case 10 look like and how many squares would it have?
- What would case 55 look like and how many squares would it have?
- Can you use 190 squares to make a stair-like structure? Justify your thinking with different representations visually, numerically, algebraically.
Low threshold, high ceiling tasks enable students to access the learning at their level of understanding. In the above example, students can spot basic numerical patterns and make connections between the cases. They can physically build and explore the growth pattern. Rich tasks such as this example can support the highest of achievers to make a generalisation and apply algebraic understanding. This approach is both supportive and challenging for students in a heterogeneous group.
What can we learn from practice in Singapore?
Singapore’s national mathematics programme is highly regarded around the world. The Singaporean syllabus places problem-solving at the very centre of the curriculum. Metacognition is the awareness of your thought process: one’s ability to think about thinking. The Mathematics Framework (Figure 3) supports students in developing the necessary concepts to problem-solve. It identifies attitudes and metacognition as key aspects in curriculum design, arguing that the learning process and students’ mindsets are important. It also fosters a mathematical approach in prioritising metacognitive development, attitudes and processes (such as thinking skills and heuristics). This provided inspiration for developments in the Junior School mathematics curriculum. Students who have increased awareness of their metacognitive processes will become more autonomous learners. Metacognition development has a significant 0.69 effect size on attainment (Hattie, 2009).
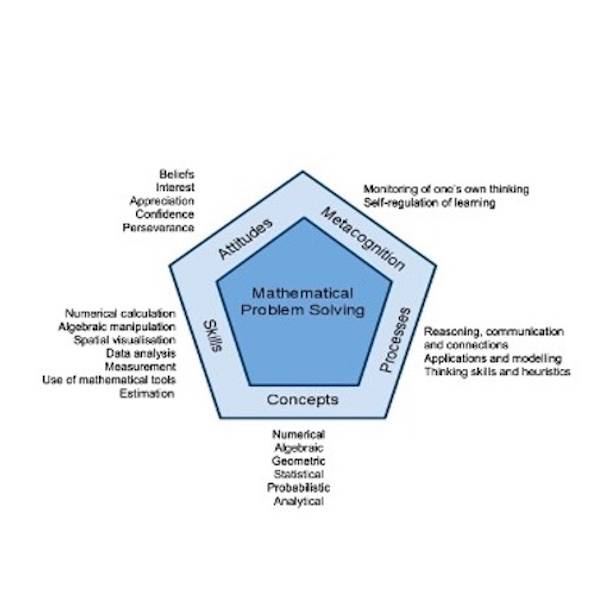
Figure 3: The Singaporean mathematics framework (Ministry of Education, Singapore, 2012)
The role of physical manipulatives in developing mathematical mindsets
Manipulatives are physical objects that can be used to represent mathematical concepts. Manipulatives are not just for infants and lower achievers. For example, place value counters can be used to help to understand the process of exchanging in addition. Algebra tiles can develop conceptual understanding, for instance physically showing the processes of substitution and collecting like terms. Manipulatives provide opportunities for children to discuss and make connections in their understanding.
Evidence shows that Bruner’s concrete, pictorial, abstract (CPA) approach (Figure 4) supports the development of mathematical mindsets and mastery of conceptual understanding. It is a key aspect of the Singapore national mathematics curriculum.

Figure 4: Concrete, Pictorial, Abstract (CPA) approach to mathematics (Maths – No Problem!, 2019)
As Andrew Jeffrey, a primary mathematics expert in the UK references, manipulatives make connections available to be noticed. Students develop the ability to reason, consider ‘why’ and justify. The deeper learning and conceptual understanding enhance their metacognition (critical participation in their own thinking and learning) and self-regulation. The use of physical manipulatives and visual representations supports the longer-term retention and application of knowledge. In the Junior School, manipulatives are used to consolidate and strengthen their understanding of formal methods for the four operations – addition, subtraction, division and multiplication. Students also explore and make connections using manipulatives in problem-solving.
Conclusion
Students who enjoy the challenge of mathematics thrive. Educators should use teaching practices in mathematics that encourage growth. The problem-solving progression developed in the Junior School facilitates the development of this mindset. It is evident that approaches which consider research in mathematical mindsets, supporting deeper conceptual understanding and practices to facilitate mastery in learning, lead to higher attainment in the subject in international assessments such as PISA, the OECD’s Programme for International Student Assessment (Johnstone-Wilder & Lee, 2010; Wathall & Erickson, 2016; Organisation for Economic Co-operation and Development [OECD], 2018) . Singapore’s syllabus and curriculum can be argued to develop mathematical mindsets, which lead to the high levels of achievement in international assessments. Students enjoy mathematics much more when they move away from memorisation and procedural repetition. Creative exploration of mathematics, and application to wider contexts and subjects, fosters a love for the subject. For instance, students can use technology, such as root robots to explore area and perimeter, and they can draw scatter graphs to explore scientific relationships. This approach embeds mathematical learning and contextualises the purpose.
A mathematical mindset encourages deeper thinking and longer-term retention of learning. This approach in the Junior School enables the students to achieve the very best outcomes possible and sets them up for future success, in secondary education and beyond.
References
Boaler, J. (2016). Mathematical mindsets: Unleashing students’ potential through creative math, inspiring messages and innovative teaching. Jossey-Bass.
Dweck, C. S. (2012). Mindset: How you can fulfil your potential. Robinson.
Efklides, A. (2008). Metacognition: Defining its facets and levels of functioning in relation to self-regulation and co-regulation. European Psychologist, 13(4), 277-287. https://doi.org/10.1027/1016-9040.13.4.277
Ericsson, K.A., Krampe, R.T., & Tesch-Römer, C. (1993). The role of deliberate practice in the acquisition of expert performance. Psychological Review, 100(3), 363-406.
https://doi.org/10.1037/0033-295X.100.3.363
Goldin, G.A. (2004). Problem solving heuristics, affect, and discrete mathematics. Zentralblatt Für Didaktik der Mathematik, 36(2), 56-60.
https://doi.org/10.1007/BF02655759
Johnston-Wilder, S., & Lee, C. (2010, September 1-4). Developing mathematical resilience [Conference presentation paper]. BERA Annual Conference. University of Warwick.
http://oro.open.ac.uk/24261/2/3C23606C.pdf
Maths – No Problem! (2019, November 6). How to move from concrete resources to abstract learning.
https://mathsnoproblem.com/blog/teaching-maths-mastery/concrete-resources-to-abstract-learning/
Ministry of Education, Singapore. (2012). Mathematics Syllabus Primary One to Six. https://www.moe.gov.sg/docs/default-source/document/education/syllabuses/sciences/files/mathematics_syllabus_primary_1_to_6.pdf
Rohrer, D., Dedrick, R.F., & Stershic, S. (2015). Interleaved practice improves mathematics learning. Journal of Educational Psychology, 107(3), 900-908. https://doi.org/10.1037/edu0000001
Schunk, D.H. (2014). Learning theories: An educational perspective (6th ed.). Pearson.
Sweller, H. (1988). Cognitive load during problem solving effects learning. Cognitive Science, 12(3), 257-285. https://doi.org/10.1016/0364-0213(88)90023-7
Wathall, J. T. H., & Erickson, H. L. (2016). Concept-based mathematics: Teaching for deep understanding in secondary classrooms. Corwin.
Yeager, D., & Dweck, C. (2012). Mindsets that promote resilience: when students believe that personal characteristics can be developed, Educational Psychologist, 47(4), 302-314. https://doi.org/10.1080/00461520.2012.722805
Youcubed. (2020). Squares to stairs.
https://www.youcubed.org/tasks/squares-to-stairs/





